For example, in economics, the game can be defined as a process of decision making. Indeed the term game theory comes from the study of the process where “players” make decisions to benefit themselves in the best possible way. Sound complicated? Well, I never said the game was easy!
To elaborate on the concept of game theory, in late 2001, a movie came out called “A Beautiful Mind”. It starred New Zealand actor, Russell Crowe, and received 4 Academy Awards, but more importantly it was a film based on the life of John Nash, a Noble Prize Laureate in the field of Economics, thanks largely to his work on game theory.
As noted above, game theory is essentially the study of decision making and, whether we realise it or not, we are all play this game of decisions every day. To illustrate, when you choose to catch the train in the morning, it is likely that you choose to catch the train that gets you to work before 9am, so you are not late for work. In this instance, your game theory is to choose the train that will result in the best outcome for your commute to work.
Just like your decision to catch the train, PPC (or Paid Search) also contains game theory. Indeed, the essentials of what a game comprises are all present in Paid Search.
- Multiple players in the form of advertisers.
- Different Strategies – different bidding strategies is just one example.
- A possible payoff that the players are competing for – top ad position for example.
Now that we have concluded that Paid Search can be treated like a game, what do we do with it?
Well, going back to John Nash and his work on game theory, there exists a principle of equilibrium also known as “Nash Equilibrium”. According to Wikipedia, the Nash Equilibrium “…is a solution concept of a non-cooperative game involving two or more players, in which each player is assumed to know the equilibrium strategies of the other players, and no player has anything to gain by changing only their own strategy.”
In short, players cannot benefit from knowing the equilibrium strategy of their opponents. A stalemate.
Let’s put this in a PPC context: with Google changing the competitive bidding policies, advertisers now find themselves in the exciting position of being able to bid on their competitors’ brand terms. At first glance, an advertiser would be crazy not to outbid their competitors on their competitors brand terms, but should they?
Well, let’s analyse this game using the Nash Equilibrium concept. Suppose that there are two large, equal sized advertisers selling similar products. In this instance, let’s call these advertisers Marco Ltd and Giorgio Inc and they sell soft drinks. Both have a PPC or paid search strategy and both are considering bidding on each other’s brand terms. Let us also assume that they actually sell products on their websites and that Paid Search is a significant revenue raising medium for both the advertisers.
Now, both of these advertisers have two strategies they can follow when it comes to competitive brand bidding. They can either bid on their competitors brand terms, or not. Here’s what the results would look like:
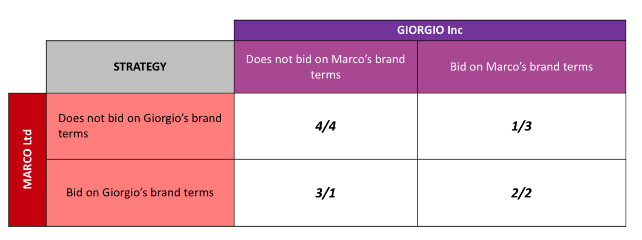
Applying Nash Equilibrium to the above situation, we can see that there are two instances where equilibrium is observed. Once when both advertisers bid on each other’s brand terms and the other one when both advertisers do not bid on each other’s brand terms.
Yet, what we can observe from this matrix is that the payoff (kept to a single digit for simplicity) is highest for both advertisers if they do not bid on each other’s brand terms, while the payoff is lowest when both the advertisers bid on each other’s brand terms.
And if only one advertiser bids on the other’s brand terms, the payoff for the one bidding is higher than the advertiser not bidding.
Therefore, logic tells us that both companies would be better off if they were to leave bidding and concentrate on their own brand terms. We know in Paid Search such competitive activity will usually lead to inflation in CPCs (Cost-Per-Clicks), which hurts return on either side of the competition.
Both bidding and not bidding is the optimal strategy, but only if the other advertiser has the same strategy.
Going back to the matrix, the highest payoff for both the advertisers occurs when both of them are not brand bidding. This would mean a mutual cooperation or agreement between both advertisers not to bid.
Now, the example of Giorgio Inc and Marco Ltd only works when both advertisers are of a similar size. But what happens when one of the advertisers is considerably smaller and has much less brand presence than the other advertiser? The situation here is slightly different.
For the larger advertiser, the situation remains largely unchanged because it has little to no incentive to bid on the smaller advertiser’s brand terms. On the flipside, the smaller advertiser will benefit by bidding on the larger advertiser’s brand terms because they are bidding to pull traffic from the larger advertiser to their own site. It may be the case that the smaller advertiser has a dominant strategy, which involves brand bidding on all occasions.
That said, there is also the opportunity to extend the application of this game to improve the SEO and Paid Search (PPC) synergies by an integration plan. Let’s think about the opportunity to calibrate the actions across these two worlds. It could be really useful to take into consideration the Markov Chains approach to leverage the SEO and finally to integrate it with the Paid Search tactics by the Game Theory.
As the paid search environment progresses, many such games will be played and while the outcomes will vary from advertiser to advertiser, overall the little guy has a chance to pull some traffic back from the bigger guy – just like Russell Crowe did when he took on the emperor of Rome in Gladiator.
